9 minute read

Introduction

I recently took an interest in Python timing attacks, specifically with the ‘==’ operator, after looking at a time-constant comparison function in a cryptography Python module. I decided that I wanted to demonstrate this attack in Python and explain it in depth here.

What are time-constant cryptography functions and why are they needed?

A great question! But first, I need to introduce how Python compares two strings using ‘==’.

As a note, when I mention time-constant, I don’t mean it in the traditional sense where regardless of the two compared strings it takes the same amount of time to return a result. Instead, I mean that for a given input size, the time it takes to return is always the same regardless of the what that fixed length input is (so it is time-constant based off length).

An analysis of the ‘==’ operation in Python

To understand how Python utilises the ‘==’ operator, we need to look at the underlying source code of Python. Python has many implementations but the most common is CPython (written in C) which I will analyse for this post. The code in question can be found here if you want to look at it in more depth, the function is ‘unicode_compare’. My C knowledge isn’t great so after some assistance from a friend (who knows C much better than me), we deciphered how this function works. To put it simply, it compares each byte in the two strings and returns False as soon as any two compared bytes are different. It repeats this a number of times equal to the length of the smallest string. If no differences were found, the code checks if the two strings differ in length and if they do not then it returns True (they are equal) otherwise it returns False. Thank you to Speakers for the help here!

As you can see, the time it takes to return a result from this comparison is not constant. The time it takes for an input of a given length is dependant on the position of the first differing byte (if any).

The issue in the cryptographic context

Lets imagine you have a client which communicates with a server, but the server requires authentication with a password before communication can start. The client sends the password to the server and the server then compares it to its stored password using ‘==’ (passwords should never be sent in cleartext like this, a secure password hashing algorithm should be used instead). The server then sends back a response a couple milliseconds later allowing the client to communicate with it. So whats wrong about this?

If the comparison finds the 1st bytes to be equal but not the 2nd then it would return False and send back a response. But if the comparison passes on the first 2 bytes and then fails on the 3rd then it would still return False but the comparison would have taken a longer period of time as an extra byte would have been compared. This would result in a slightly later response from the server. An attacker can take advantage of this fact and send multiple brute force attempts (assuming there is no rate limiting in place) to the server to guess the password character by character. Should the server return a response significantly slower than the rest, then it means the character is likely correct at that position. Given enough time, an attacker could potentially brute force a password utilising this timing attack.

How would we fix this?

This is where time-constant functions come into play. If a function takes the same amount of time to return a result regardless of how many bytes match at the beginning, then it would not be possible for an attacker to brute force each character one by one. To do this, we need to make the comparison take the same amount of time regardless of how many bytes are correct so it cannot return False as soon as two bytes are different. When applied, if an attacker tries the same timing attack, then no character should return slower than another, meaning the password cannot be brute forced using this method!

Nate Lawson wrote an article explaining how to fix this type of vulnerability. Their code can be found below:

1
2
3
4
5
6

  if len(s1) != len(s2):
    return False
  result = 0
  for x, y in zip(s1, s2):
    result |= ord(x) ^ ord(y)
  return result == 0

The code above first checks the length of the two inputs, returning False if they are different. Then it loops through each character, like before. The difference this time is that it doesn’t stop as soon as it finds a different character. It instead goes through each character in each string and performs a bitwise XOR on them. If they are the same, then the returned result would be 0. By utilising a bitwise OR with the result variable, if at any point the XOR operations returns a non-zero result, then the result variable will be non-zero, causing a False to be returned after every character has been checked.

It is important to mention that using this approach, an attacker can still brute-force the length of the password, but as long as the password is of a sensible length, it should not be an issue.

Why isn’t this constant-time comparison used for the Python ‘==’ operator?

Although the time-constant comparison is more secure in a cryptographic context, from a performance standpoint, it is not suitable performance wise. This is because it is more efficient to return as soon as a difference is found rather than iterate over every character regardless of if a difference is found. For strings of a small length, this isn’t an issue but it becomes an issue for larger comparisons.

Requirements

I will present a Python timing attack below. But first, I must go over the requirements of the program.

The program will have a fixed ‘password’ value in the program which will be randomly generated from 5 lowercase ASCII characters. Utilising a timing attack against the ‘==’ operator, I will find the password through attempting to brute force each character in the password. I don’t expect the program give the correct output every time it is ran (due to some possible processing noise during the time analysis) but I expect the majority of outputs to be correct.

Why do I use a fixed length password?

The main reason is output time. A password of length 10 will take twice as long to find as a password of length 5. Additionally, a lower password length also reduces the chance of a false positive occurring which is when a letter is incorrectly thought to be the correct letter due to some disruption / delay in processing the comparison.

The methodology

Feel free to skip this section as it just highlights my methodology. The actual attack will be displayed in the next section.

Measuring the times

The program will loop through every lowercase ASCII letter and try to find the letter which takes the longest to return. The program will utilise the timeit module to time how long a comparison between two variables takes. It will utilise two timings: the time it takes to process a control input and the time it takes to process a guess input. The control input contains all previously correct ASCII characters (none if guessing the first letter). The guess input contains all previously correct ASCII characters along with a new guess character. If the guess input takes a longer amount of time to process than the base input then it is possible that the guess input’s new letter is in a correct position.

The idea above was mainly taken from not1cyyy’s timing attack implementation which can be found here.

Confidence levels

Lets say that we are trying to guess the character in the 1st position of the password. On the first loop over the 26 ASCII letters, if any letters are likely to be in a correct position (when their guess time is higher than their base time), then their confidence rating is increased by one. This repeats for each subsequent loop. If a letter is skipped 2 times in total for the current character position, then it loses confidence and is skipped in subsequent loops, leaving the remaining letters as possibilities.

Eventually after enough loops, the number of letter possibilities should tend towards 1, where the remaining character is most likely correct at that position. The reason for giving each letter 2 chances it due to processing noise as if the correct letter happens to hit a false negative then it gives it one extra chance before it loses confidence.

The attack itself

It roughly takes 3 and a half minutes to execute the attack on a good run (where no letters are guessed wrongly).

Below is a run of the program. In this example, the password is a random combination of 5 lowercase ASCII letters. The image below showcases the first character guess.

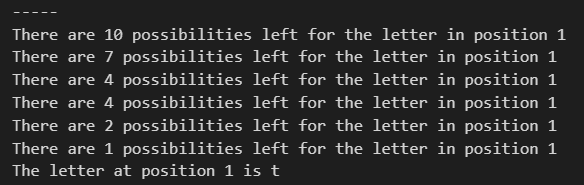
Guessing the first letter

After a few initial loops, the program starts outputting the number of possibilities that are remaining based off their confidence level. After the number of possibilities is reduced to 1, this letter is assumed to be the correct letter and so it placed at the first position of the guessed password.

It repeats this process until the last letter, at which point, the program just loops through all 26 ASCII characters until the password is found as seen below.

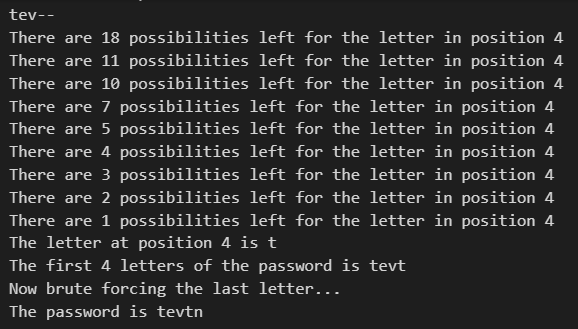
Guessing the last letter

This is done not only because it is faster than utilising the previous method to find the last letter, but also because utilising the previous method doesn’t actually work for the final letter (likely due to how Python implements its comparison). As you can see, the randomly generated 5 letter password was tevtn.

The source-code for my attack can be found on my GitLab page here.

Does this attack work remotely?

My implementation of this attack occurs locally on my system, you may realise that there isn’t much use for this for an attacker (unless they are trying to brute-force entry into a locally running program). What would really be useful is if this attack would work remotely. Considering the fact that my implementation of the attack sometimes fails due to background processor noise, you may think that with the added noise of network transmissions that a remote attack would not be possible.

Unfortunately, it is possible. This paper showcases that a timing attack is possible over the internet. This is why it is exceedingly important for all software written in the cryptographic context to have a time-constant comparison function.

Conclusion

Overall, I found working on this exploit very fun and it highlighted the importance of time-constant comparison functions. During the implementation I did try to configure the attack to work over a Python Flask localhost connection, but I could not get this to work due to system latency and also because I was trying the attack on Windows (which has limitations with the accuracy of measuring time). Perhaps I can re-visit this project at some point in the future to implement this remote capability.

References

Below are some resources that I used for this project:

Disclaimer

All information provided on this post is for educational purposes ONLY. DO NOT attempt to use any of this information for illegal purposes. I take no responsibility for how information on this website is used. Any actions or activities commited by you utilising the information on this site is solely your responsibility.